GAN Metrics

Inception Score

Concept 用图片分类器来评估生成图片的质量。清晰度：对于清楚的图片，分类器应该可以确定的判断该图的种类，那么其熵$p(y|x)$（即不确定性）比较小。多样性：对于所有生成的图片，每个种类应该均匀生成，所以$p(y)=\sum p(y|x^{(i)})$
Equation： $IS(G)=\exp(\mathbb{E}_{x\sim p_g}D_{KL}(p(y|x)||p(y)))$
- $\mathbb{E}_{x\sim p_g}$: 循环所有样本
- $D_{KL}$: KL散度
- $p(y|x)$: 对于图片x，属于所有类别的概率分布，对于给定图片x，表示为一个1000维向量
- $p(y)$: 边缘概率，具体实现为对于所有的验证图片x，计算得到$p(y|x)$，再求所有向量的平均值。
IS 有什么问题
1. 数据集，因为基于InceptionV3，只能使用ImageNet1000，所以不能直接生成图片套用在InceptionV3上。
2. 使用框架的不同，pytorch，tensorflow等，IS差别会很大
3. IS高的图片不一定真实：因为是根据分类器来给分的，所以可以根据分类器的结果来刷分（提高全体图片的类别多样性，那么每一张图片的熵就会低）
4. IS低的图片不一定虚假：如果图片的类不在1000类中则会低
5. 多样性检测有局限性：如果每个类只生成一个样子，依旧是mode collapses
6. IS不能反映过拟合：如果模型完全记忆数据集，给出Train集的数据，IS也会很高。

FID

Definition: The Frechet distance $d(\cdot,\cdot)$ between the Gaussian with mean $(m, \Sigma)$ obtained from $p(\cdot)$ and the Gaussian with mean $(m_r, \Sigma_w)$ obtained from $p_w$. 假设原始图片和生成图片都服从高斯分布，计算两个分布的均值和协方差，算均值和协方差的距离。
Equation: $d^2((m_g, \Sigma_g), (m_r, \Sigma_w) = ||m_g-m_r||^2_2 + Tr(\Sigma_g+\Sigma_w-2(\Sigma_g\Sigma_w)^{0.5})$

Method:

1. 加载图片[B,C,H,W], 文件数最好是bs的倍数否则会导致少读几个文件。
2. Inception V3去除输出层，只取到最后一个pooling层，
    得到[Bx2048x1x1] feature（如果输入图片尺寸不对，
    增加一个adaptive_avg_pool2d到1x1)
3. diff = m_g-m_r
    diff.dot(diff)+np.trace(sigma_g)+np.trace(sigma_r)-2*linalg.sqrtm(simga_g.dot(sigma_r))

FID 优缺点
1. 优点1：生成模型的训练集可以和InceptionV3不同
2. 优点2：刷分不会导致生成图片的质量变差
3. 缺点1：强假设提取的图片特征符合Gaussian
4. 缺点2：无法反映过拟合的问题

LPIPS(Learned Perceptual Image Patch Similarity)

$d(x,x_0)=\sum_l \frac{1}{H_l W_l} \sum_{h,w}||w_l \bigodot (\hat{y}^l_{hw}-\hat{y_{0}}^l_{hw})||$
通过预训练的VGG，AlexNet等网络，对一对图片x,x_0进行特征提取，对每层提取出来的特征计算归一化后相减得到diff并平方（？），将每层的diff过一个1x1的卷积（乘以w），并进行空间尺度上的平均，最后每层的输出相加。
StarGANv2里使用LPIPS来测量多样性，数值越大说明越不相似。
- 对此存疑，原文中是通过训练一个simple network，将diff的结果输入到这个网络中让他判断是原图和distort图一对，来反过来finetune整个pretrained network。但是starganv2里好像直接采用了vgg的网络？

Precision and Recall（Improved）

Motivation: 因为IS，FID等只有一个维度的分数，所以无法区分不同失败的例子。（无法同时满足真实性和多样性两个指标）
Definition: 对于参考分布P(X)和学习到的分布Q(Y)，
- Precision: 生成的图片可以落在真实分布的流型上的比例 $\frac{1}{M}\sum_{j=1}^{M} 1_{Y_j \in \text{manifold}(X_1,...,X_N)}$
- Density: 真实的图片覆盖生成分布的比例 $\frac{1}{N}\sum_{i=1}^{N} 1_{X_i \in \text{manifold}(Y_1,...,Y_M)}$ 其中N,M是真实和生成的数量，流型Manifold定义为： $\text{manifold}(X_1,...,X_N)=\bigcup_{i=1}^{N}B(X_i,\text{NND}_k(X_i))$ 其中$B(x,r)$是以x为球心，r为半径的D维球形；$\text{NND}_k(X_i)$是$X_i$到除了自己以外第k近的邻居的距离。

Density and Coverage

Motivation:precision和recall会受到outliers的影响且计算效率低。
- outlier: 在没有归一化操作前，一个outlier会使得得到的流型覆盖一大块在outlier附近的区域，从而让流型overestimate。
  - precision: 生成的样本可能落在overestimate的流型部分中从而让percision看起来更高。
  - recall：因为模型倾向于生成不真实但不同的样本，所以生成流型也经常比真正的生成分布大。另外由于每个模型的fake manifold都不同，每次都需要重新计算流型。
- computational inefficiency：需要两两计算距离，每个样本都需要计算$O(kM\log M)$
于是提出了Density和Coverage
- Density：计算有多少个真实样本的neighborhood sphere包含$Y_j$, $\frac{1}{kM}\sum_{j=1}{M}\sum_{i=1}{N}1_{Y_j \in B(X_i, \text{NND}_k(X_i))}$
- Coverage:计算所有真实样本中，neighborhood sphere包含至少一个生成样本的比例。 $\frac{1}{N}\sum_{i=1}^{N}1_{\exist j \text{s.t.} Y_j \in B(X_i, \text{NND}_k(X_i))}$
mode collapse 和 mode dropping的区别？
- mode collapse是 many z to ~one x
- mode dropping是 real data not inG(z)

Perceptual Path Length

Idea：除了清晰度和多样性，生成器能否很好的把不同图片的特征分离出来也是一个关注的指标。StyleGAN的作者希望当我们给定一个z from latent space的时候，$z_1$能控制人的头发，$z_2$能控制人的眉毛等等，当调整$z_1$时，生成的图片只会有头发的变换。
Equation: PPL评估利用生成器从一个图片变到另一个图片的距离，越小越好
- $\epsilon$ 细分的小段，1e-4
- $d(\cdot,\cdot)$ perceptual distance，用预训练的VGG来衡量
- slerp：spherical linear interpolation球面线性插值
- $t\sim U(0,1)$插值参数，服从均匀分布

Generative Adversarial Network、

WGAN

书接JS散度
考虑到几乎不可能去便利所有的联合分布$\gamma$去计算距离$||x-y||$的期望$\mathbb{E}_{(x,y)\sim\gamma}[||x-y||]$，因此直接计算$W(p_r, p_g)$是不现实的，WGAN提出用 Kantorovich-Rubinstein 对偶性将W转化为：

$W(p_r, p_g) = \frac{1}{K}\sup_{||f||_L \leq K} \mathbb{E}_{x\sim p_r}[f(x)]-\mathbb{E}_{x\sim p_g}[f(x)]$

$\sup(\cdot)$是上确界，$||f||_L \leq K$表示函数$f: R\rightarrow R$满足K-阶Lipschitz连续性，即满足

$|f(x_1-x_2)| \leq K\cdot |x_1-x_2|$

于是，我们使用判别网络$D_\theta (x)$参数化$f(x)$函数，在$D_\theta$满足1阶Lipschitz约束的条件下，K=1，得到：

$W(p_r, p_g) = \sup_{||D_\theta||_l \leq 1} \mathbb{E}_{x\sim p_r}[D_\theta(x)] - \mathbb{E}_{x\sim p_g}[D_\theta(x)]$

因此求解$W(p_r, p_g)$的问题转化为：

$\underset{\theta}{max}\mathbb{E}_{x\sim p_r}[D_\theta (x)] - \mathbb{E}_{x\sim p_g}[D_\theta (x)] \;\;\;\text{such that}\;\; \ ngledown_{\hat{x}}D(\hat{x}) \leq I$

也就是在满足D(x)处处导数小于1的情况下求解最大值。所以在实际应用上作者的做法是，限制神经网络的所有参数$\theta$都不会超过某个范围[-c,c]，这样关于输入样本x的导数$\frac{\partial f_\theta}{\partial x}$也就不会超过这个范围，所以通过这个上届，满足小于某个K值的上确界。

可以防止mode collapse，但不能提升图像质量。

WGAN-GP

添加了Gradient Penalty来迫使判别器满足1阶Lipschitz函数约束，同时发现在1周围工作效果更好

$\text{GP} \triangleq \mathbb{E}_{\hat{x}\sim P_{\hat{x}}}[(||\triangledown_{\hat{x}}D(\hat{x})||_2 - 1)^2]$

所以Discriminator的目标函数为：

$\underset{\theta}{max} \mathcal{L}(G,D) = \mathbb{E}_{x_r\sim p_r}[D(x_r)] - \mathbb{E}_{x_f\sim p_g}[D(x_f)] -\lambda\mathbb{E}_{\hat{x}\sim P(\hat{x})}[(||\triangledown_{\hat{x}}D(\hat{x})||_2-1)^2]$

第一项是EM距离，第二项是GP，其中$\hat{x}=tx_r+(1-t)x_f,\;\; t\in[0,1]$
Generator的目标函数为：

$\underset{\theta}{min} \mathcal{L}(G,D) = \mathbb{E}_{x_r\sim p_r}[D(x_r)] + \mathbb{E}_{x_f\sim p_g}[D(x_f)]$

又第一项与G无关，可以省去得到

$\underset{\theta}{min} \mathcal{L}(G,D) = -\mathbb{E}_{x_f\sim p_g}[D(x_f)] = -\mathbb{E}_{z\sim p_z(\cdot)}[D(G(z))]$

WGAN做了什么？
- 判别器去掉最后一层sigmoid
- discriminator和generator在算loss时没有log
- 每次更新判别器的参数后把他们的绝对值clip到一个孤单常数c
- 不使用Adam等基于动量的优化算法，推荐使用RMSProp，SGD也行
为什么WGAN要把vanilla GAN的最后一层sigmoid拿掉
- 因为原始的GAN的目标是判断图片的真假，所以用sigmoid来获取类别的概率。WGAN中判别器作为EM距离的度量网络，其目标是衡量生成分布$p_g$和真实分布$p_r$之间的EM距离，属于实数空间，所以不需要加Sigmoid。

Vanilla GAN

Idea: 给定一个latent z使用generator来生成图片，使用discriminator来判断区分生成图片和真实图片，并返还gradient给Generator更新参数。Discriminator的目标是最大化区分真假的结果，Generator的目标是最小化其生成图片被判断为假的概率。最后两者大道纳什均衡。
Equation:
- Discriminator:
  $\mathcal{L}(G,D)=\mathbb{E}_{x_r\sim p_r}[\log D(x_r)]+\mathbb{E}_{z\sim p_z}[\log(1-D(G(z)))]$
- Generator:
  - 因为$\log(1-D(G(x)))$的梯度很小，作者用了一个log D trick，将其替换为最大化$\log(D(G(x))$，其梯度更大，且和Discirminator学习的方向一致。
- 所以总的目标函数为：
  $\underset{G}{min}\ \underset{D}{max}\ V(G,D) = \mathbb{E}_{x_r\sim p_r}[\log D(x_r)]+ \mathbb{E}_{z\sim p_z}[\log D(1-G(z))]$
Vanilla GAN的问题
- 判别器越好，生成器梯度消失越严重。
  - 当固定G的时候D Loss变为：$-P_r(x)\log(D(x))-P_g(x)\log(1-D(x))$
    令其关于D(x)的导数为0的道 $-\frac{P_r(x)}{D(x)}+ \frac{P_g(x)}{1-D(x)}=0\\ D^*(x) = \frac{P_r(x)}{P_r(x)+P_g(x)}【2】$ 论文里于是证明：当$P_r(x)=0$且$P_g(x)\neq0$时，最优判别器应该为给出0（也就是说判断生成的图片都为假）；而当$P_r(x)=P_g(x)$时，最优判别器应该给出0.5（也就是说无法判断谁真谁假）
  于是我们回头看Generator的loss，加上一项判断$x_r$的值对于gradient并无影响(最小化他等同于最小化之前的loss），得到：
  
  把公式【2】带回，得到
  
  根据JS散度:
  
  在假设中JS散度对于有重叠的两个分布则公式是成立，但是因为GAN的z的取值有限（比如2^6维）而要生成的图片维度极高（比如256*256=2^16），则图片虽然在高维，但是其变化受到z值的限制，于是两个$p_r$和$p_g$的分布就很难会有重叠；如果没有重叠，那么JS散度就变成了0，而损失也就变成了-2log2，而梯度就变成了0。
- 最小化第二种生成器loss函数，会等价于最小化一个不合理的距离衡量，导致两个问题，一是梯度不稳定，二是mode collapse。
  经过推导，最小化第二个G loss函数等同于最小化 $KL(P_g||P_r)-2JS(P_r||P_g)$ 一边是要最小化生成分布和真实分布的KL散度，另一边却又要最大化两者JS散度，于是会梯度不稳。另外，$KL(P_g||P_r)$项对生成的样本不真实时惩罚巨大，对没生成真实样本的情况惩罚微小，导致生成器偏向生成几种确定的样本，从而导致模式坍塌。

LSGAN

$L_D^{LSGAN}=\mathbb{E}[(D(x)-1)^2]+\mathbb{E}[D(G(z))^2]$ $L_G^{LSGAN}=\mathbb{E}[D(G(z)-1)^2]$

惩罚离群的点，让生成图像接近真实数据
但是会使得生成图像失去多样性

DCGAN

把GAN的mlp转变为全卷积。Generator里用Conv2dTranspose进行上采样，一步一步扩大图片尺寸。
- Generator中使用ReLU作为激活函数
Discriminator和Generator对称，取消pooling层，用带步长的卷积代替，一步一步缩小图片，最后判断图片真假。
- Discriminator中使用Leaky ReLU。
Generator和Discriminator中使用BN层（稳定GAN的训练）
- 实验表示但不要对generator的输出层和discriminator的输入层使用BN，会不稳定
提出latent interpolation，对于z1，z2生成的两张图片x1，x2，如果对z1，z2进行线性插值生成的图片应该显示从x1逐渐渐变到x2。如果图像发生急剧变化，则就是模型没有学到特征只是记住了图像。
通过生成模型输入向量的加减发修改图像，类似word2vec，king-man+woman=queen

Improved Techiques for Training GANs

Feature matching: 因为generator和discriminator在进行min max的纳什均衡游戏，但是两者的目标函数又是凹函数，会导致两者loss此消彼长。提出使用discriminator作为feature extractor，然后将generator的目标改为$||\mathbb{E}_{x\sim p_r}f(x)-\mathbb{E}_{z\sim p_z}f(G(z))||_2^2$。
- 个人认为虽然在统计意义上是合理的，但是不是很make sense，在多轮epoch中一张图片会有不同z生成，势必导致G混淆latent的作用。
Minibatch Discriminator：认为mode collapse的原因和discriminator每次只看一张图片有关，由于每次只看一张图片，discriminator容易落入local minimal无法跳出。所以使用minibatch，对于discriminator中间的一层输出，每个图的特征$x_i\in minibatch$通过一个矩阵T，映射成一个矩阵。然后每个图对应的矩阵的第k行两两做L1距离的计算并求和，然后重新组成一个n x B的矩阵作为下一层的输入。
- 后来的文章基本没有用这个方法。
Historical averaging 生成和判别器的损失函数中添加一项正则项，$||\theta-\frac{1}{t}\sum_{i=1}^{t}\theta[i]||^2$，通过保证和之前的参数的抖动不过大来控制GAN的稳定性（后来的文章几乎也没见过，有使用衰减系数来记录参数的）
One-side Label Smoothing
Virtual Batch Normalization
提出了IS ，感觉是本文唯一被引用的原因。

Conditional GAN

在Vanilla GAN的基础上添加了条件概率，使得目标函数变为

$V(G,D) = \min_{G} \max_{D}\mathbb{E}_{x\sim p_x}[\log D(x|y)] + \mathbb{E}_{x\sim p_g}[log(1-D(x|y))]$

具体操作中就是

把输入的z和类别c做concat，作为输入给generator
把$x$和c作为输入给到判别器，让他判断（1）x是否是真实的，（2）x是否属于类别c

Pix2Pix

Generator：使用Unet结构，输入的轮廓图x进行encode，然后再decode成图片
- Unet：输入和输出的图像的surface appearance应该不同，而潜在的结构（underlying structure）应该相似。对于I2IT的任务来说，输入和输出应该共享一些底层信息，因此使用Unet这种跳跃连接（skip connection）的方法，i层与n-i层concat。
Discriminator：使用条件判断器PatchGAN，将图片变成70x70的区块并判断每个区块的真假并统计。
- 因为L1和L2 loss重建的图像很模糊，并不能很好的恢复图像的高频部分（图像的边缘等），而对于低频部分（色块等）恢复良好，所以采用patch的方式分区块对局部进行判断。
Loss Function $\arg\min_G \max_D \mathbb{E}_{x,y}[\log D(x,y)]+\mathbb{E}_{x,z}[\log(1-D(x,G(x,z)))]+\\\mathbb{E}_{x,y,z}[||y-G(x,z)||_1]$
作者认为L1 loss可以来补充低频信息，而GAN Loss可以来补充高频信息
缺点：x到y之间是一对一的映射，应用范围有限，且test的数据与train数据差距较大时效果很差。

BicycleGAN

为了增加多样性

VAE-GAN

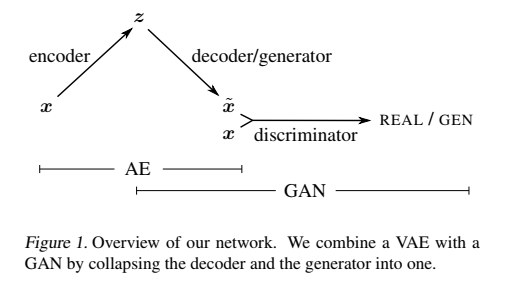
图片压缩成z，再还原成图片最后GAN loss判断
cVAE-GAN
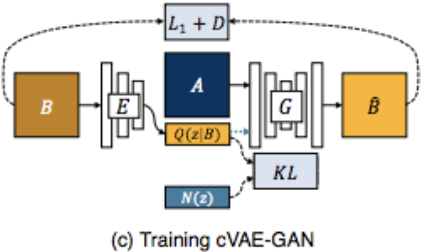
- 不变的是：
  - L1 和 D的loss
  - 从 B到 z 再到B
- 在VAEGAN的基础上添加了
  - 压缩的z和随机采样的z做kl损失，使得压缩的z符合随机分布
  - Generator take A and z as input
cGAN
- 将class和latent concat作为输入给generator
cLR-GAN
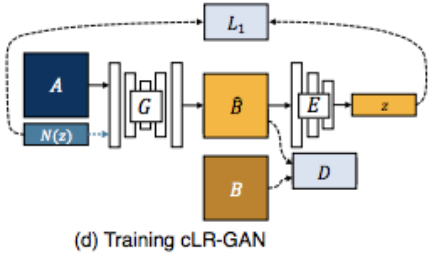
- 不变的是：
  - A对应的就是y， z还是随机的变化，作为G的输入
  - 真实B和生成的B做D的判断
- 在cGAN的基础上添加了
  - Encoder，并重新压缩B得到$\hat{z}$和z做L1 loss
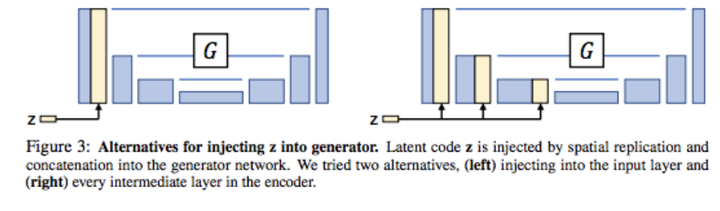
Unet中z有两种concat的方法：