从VAE到GAN

Overview

我们可以大致把模型分为两类

• Discriminative Model 判别模型
• Generative Model 生成模型

判别模型中，比如分类模型，就是求解最大化后验概率，即直接对后验 $p(C_k|x)$ 建模，显性或隐性地求出其表达式

$$label = \underset{k}{arg\:max}\;p(C_k|x)$$

而生成模型中，则需要直接或间接对p(x)建模：

$$\begin{align} label &= \underset{k}{arg\:max}\;p(C_k|x)\\\\ &=\underset{k}{arg\:max}\;\frac{p(x|C_k)p(C_k)}{p(x)} \\\\ &=\underset{k}{arg\:max}\;p(x|C_k)p(C_k) \end{align}$$

AutoEncoder

比方说我们有一堆图像数据x，通常FC，CNN的等做法是通过我们设计的神经网络中的隐藏变量，判断标签，然后反向传播误差学习并不断调整这些隐藏变量。$x \rightarrow z \rightarrow classifier$ 而这些隐藏变量就是一些我们理解或无法理解的特征。这一步相当于是一个encoder，把数据编码成特征。

换一种思路，我们可以直接利用这些隐藏变量直接来，$x \rightarrow z \rightarrow \hat{x}$ ，然后我们再比较学习L2 loss_function $\mid\mid(\hat{x}-x)\mid\mid^2$。这个过程中，我们相当于通过学习到的一些隐藏特征重建图片，然后再和原图对比。这一步相当于是一个decoder，把特征解码还原成数据。

通过一段时间的学习后，我们可以把 $z\rightarrow \hat{x}$ 的连接(decoder)去掉，重新换成普通的classifier，与输入的标签配合起来，$x \rightarrow z \rightarrow classifier$。这样只需要少量的数据我们就可以完成一个判断模型了。

Variational AutoEncoder

目标

我们希望有一个模型能生成我们想要的数据。

这是一个概率版本的AutoEncoder，通过对模型抽样来生成数据。举例来说，这就是像是我们讲高斯分布时的那个小球实验，模型就是那个充满柱子的板，而每一个小球就是一次抽样，通过足够多的抽样，我们就可以生成一个类似的高斯分布。

接着我们可以假设，万物皆有规律，存在着一些隐藏变量z，控制着如何生成我们的数据。当然还有一些全局变量 $\theta$ 也影响着我们的x和z。

那么，根据上面的描述，相互作用的关系如下图所示

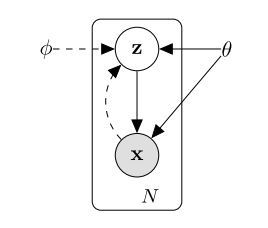
所以从先验 $\theta$ 中采样 $p_{\theta^{ }}(z)$，采样x的概率为 $p_{\theta^{ }}(x \mid z^{(i)})$。

因为我们不知道z究竟是啥，那么就请出万能的高斯分布使得z服从高斯分布。

但是建立在隐藏变量z上的x的概率p(x|z)就比较复杂了，我们可以使用神经网络来表示它，也就是说，在 $z \rightarrow x$ 中加一个Decoder Network变成， $z \rightarrow Decoder\;Network \rightarrow x$

根据全概率公式，数据x的概率可以表示为

$$p_{\theta}(x) = \int p_{\theta}(z)p_{\theta}(x|z)dz$$

在上式中，$p_{\theta}(z)$ 我们已经假设成一个简单的高斯先验了，$p_{\theta}(x|z)$ 我们假设成了一个希望学习的神经网络，但是问题就出在积分上，我们很难对每个z值都去计算p(x|z)，所以直接对p(x)建模这条路走不通了。

那么再看一下后验分布

$$p_{\theta}(z|x) = \frac{p_{\theta}(x|z)p_{\theta}(z)}{p_{\theta}(x)}$$

其中 $p_{\theta}(x|z)$ 和 $p_{\theta}(z)$ 如上，但是问题出在分母 $p_{\theta}(x)$ 上，原因同上。显然这条路也走不通。

仔细一看，$p_{\theta}(x|z)$ 和 $p_{\theta}(z|x)$ 不就是我们autoencoder中的解码器decoder和编码器encoder么？

那么既然 $p_{\theta}(z|x)$ 我们求不出，不如换个思路找一个接近它的 $q_{\phi}(z|x)$，这一步就是变分推断Variational Inference。

Variational Inference 变分推断

直观理解

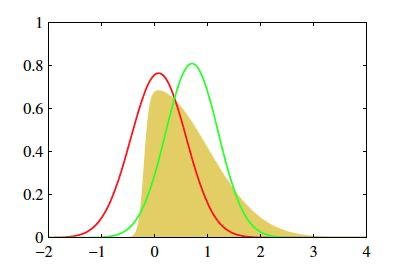
对于上图图的黄色分布p（我们观测到的数据），我们希望能找到一个相近的分布q，尽量使得猜测的分布和黄色分布重合。

具体步骤

1. 我们拥有两部分输入：数据 $X$ 和模型 $p(z,x)$
2. 目标是求后验概率 $p(z|x)$ ，但是不能直接求。

3. 我们构造一个后验概率 $p(z|x)$ 的近似分布 $q(z;v)$

   • 如何构造q(z;v)？
   • 我们知道p的分布是高斯分布，那么可以假设q同样是高斯分布（其实用exponential family的分布也行）
4. 误差用KL散度计算，用ELBO不断缩小逼近q和p之间的距离直至收敛。

回到VAE的问题来

既然假设了p和q两个是解码器和编码器，我们可以做如下建模：

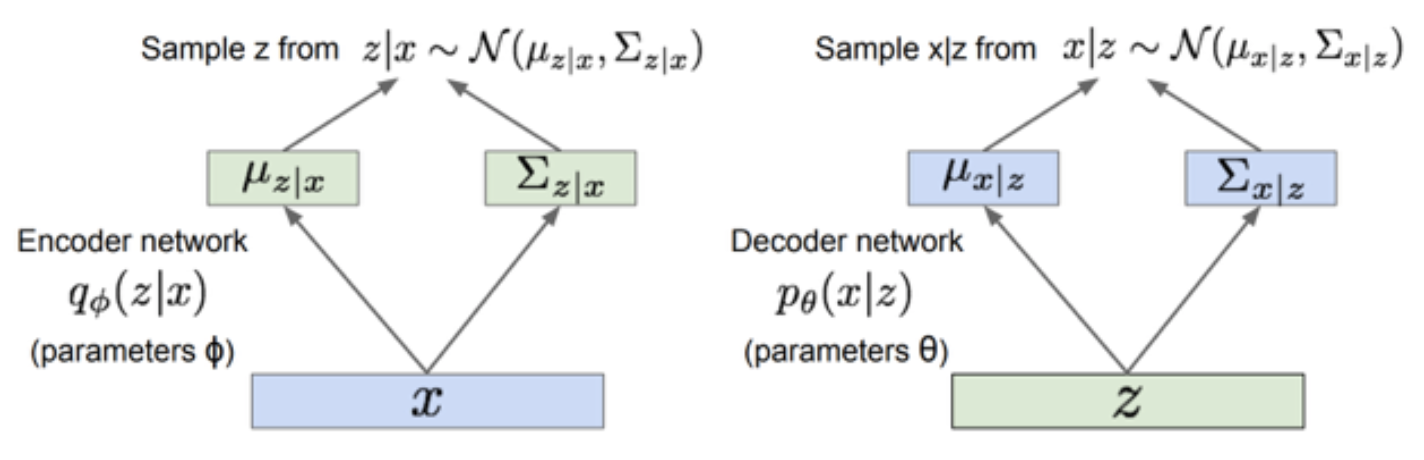
其中 $\Sigma$ 是标准差组成的对角矩阵。而在里面，我们用 $q(z|x)$ 来接近 $p(z|x)$，所以q分布属于exponential family，$q_{\theta}(z∣x)$。 假设p是高斯分布，则q也可以假设为高斯分布。

所以我们的log data likelihood:

$$\begin{align} log\:p_{\theta}(x^{(i)}) &= E_{z\sim q_{\phi}(z|x^{(i)})}[log\:p_{\theta}(x^{(i)})]\\\\ &= E_z[log\frac{p_{\theta}(x^{(i)}|z)p_{\theta}(z)} {p_{\theta}(z|x^{(i)})}]\\\\ &= E_z[log\frac{p_{\theta}(x^{(i)}|z)p_{\theta}(z) q_{\phi}(z|x^{(i)})} {p_{\theta}(z|x^{(i)})q_{\phi}(z|x^{(i)})}]\\\\ &=E_z[log\:p_{\theta}(x^{(i)}|z)] - E_z[log \frac{q_{\phi}(z|x^{(i)})}{p_{\theta}(z)}] + E_z[log \frac{q_{\phi}(z|x^{(i)})}{p_{\theta}(z|x^{(i)})}] \\\\ &=E_z[log\:p_{\theta}(x^{(i)}|z)] - \mathbb{KL}(q_{\phi}(z|x^{(i)})||p_{\theta}(z)) + \mathbb{KL}(q_{\phi}(z|x^{(i)})||p_{\theta}(z|x^{(i)})) \end{align}$$

好了，我们来看一下每一项

• $E_z[log\:p_{\theta}(x^{(i)}|z)]$ 可以通过解码器 $p_{\theta}(x|z)$ 计算估值。
• $\mathbb{KL}(q_{\phi}(z|x^{(i)})||p_{\theta}(z))$ 这个KL散度求的是encoder的高斯分布和先验z的熵差，不难求。
• $\mathbb{KL}(q_{\phi}(z|x^{(i)})||p_{\theta}(z|x^{(i)}))$ 这个散度无法求，但是我们知道KL散度一定大于等于零

前两项就组成了可以计算的下界

$$\mathcal{L}(\theta, \phi; x) = \\\\ E_q[log\:p_{\phi}(x,z)] - \mathbb{KL}(q_{\phi}(z|x^{(i)})||p_{\theta}(z))$$

也就是ELBO

$$log\:p_{\theta}(x^{(i)}) \geq \mathcal{L}(\theta, \phi; x)$$

我们的目标是最大化ELBO下界。

回到神经网络来

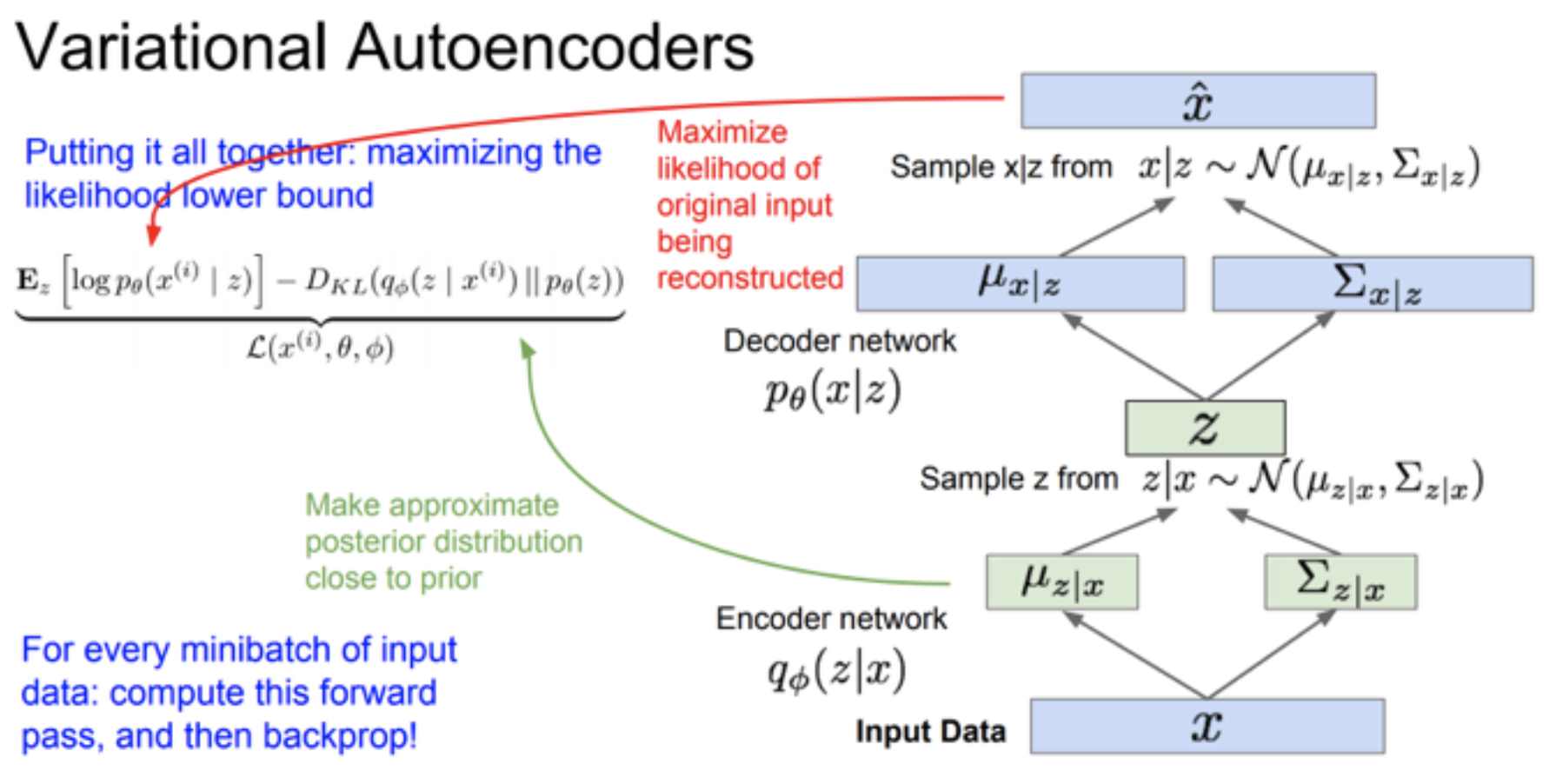
我们从下往上捋。

1. 输入是x
2. 通过encoder network，我们得到对应的 $\mu$ 和 $\Sigma$
3. 因为我们假设 $q_{\phi}(z|x)$ 服从高斯分布，所以我们就可以得到$q_{\phi}(z|x) = \mathcal{N}(z|\mu(x;\theta),\sigma(x;\theta))$
4. 已知z也是服从高斯分布的，那么可以根据KL散度计算第二项了
5. $z=q_{\phi}(z|x)$
6. 把得到的z通过decoder network，得到 $\hat{x}$，也就是我们构造出来的数据
7. 那么第一项也可以计算了 $$\begin{align} E_q[log\:p_{\phi}(x,z)] &= E_q[log\:\mathcal{N}(x|f(z;\theta,\sigma^2I))] \\\\ &=||x-f(z;\theta)||^2 \end{align}$$

这样我们就算出了一组数据下界，然后可以反向传播。

VAE:
    全连接层fc1 shape(input_size, 400)
    两个相同的连接层fc21, fc22 shape(400, latent_size)， 一个给mu，一个logvar
    再一个全连接层fc3 shape(latent_size, 400)
    最后变回原来的size fc4 shape(400, input_size)

VAE encoder： 返回 fc21(Relu(fc1(x)) , fc22(Relu(fc1(x))

VAE decode: Sigmod(fc4(Relu(fc3(z))))

VAE forward:
    Input x # 对应1
    mu, logvar = encode(x) # 对应2
    z = reparameterize(mu, logvar) # 对应3，5
    reconstructed_x = decode(z) # 对应6
    Return reconstructed_x, mu, logvar

每个epoch：
    每个batch中：
        reconstructed_x, mu, logvar = VAE.forward(x) # 正向传播
        Loss = loss_function(reconstructed_x, x, mu, logvar){          # 计算loss
            crossEntropy = F.binary_cross_entropy(reconstructed_x, x.flatten, reduction='sum’) #等式右边部分，对应7
            kl_divergence= -0.5 * torch.sum(1+logvar-mu**2-torch.exp(logvar)) #等式左边部分，对应4
            Return crossEntropy + kl_divergence
        }
        Loss.backward() # 反向传播
        Optimizer.step() # 梯度下降

Reparameterize Trick

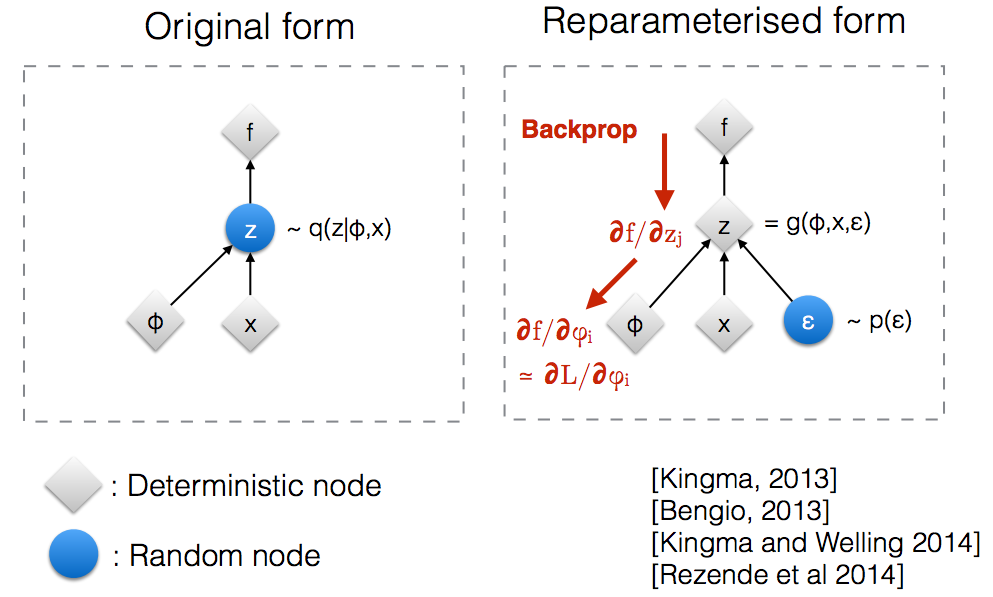
如果直接用z作为隐藏函数，那么在反向传播时会被阻断。把z分解为 $\mu$ 和 $\sigma$，方便梯度传播

VAE reparameterize：eps ~ N(0 , e ^ (0.5 * logvar)), 返回 mu + eps*std

GAN Generative Adversarial Network

在VAE中我们看到了如何用decoder从隐藏变量生成 $\hat{x}$，那么我们换一个思路，能不能直接让一堆噪声z，生成 $\hat{x}$。再去通过比较拥有的数据图片，进行学习。

于是我们就有了生成对抗网络。顾名思义，这个网络有两部分组成，Generator和Discriminator。

生成器就和VAE中的decoder一样。而Discriminator就和CNN网络一样。想法是，我们生成的图片一定是假的，而喂的图片是真的，通过Discriminator来判断那些图是真的，那些图是假的，并通过判断的结果反向传播给Generator让他不断进步，直到Discriminator无法再分辨我们的生成的图片是真是假（为什么是0.5？如果直接全部判断为真，那说明这个判别器被overtrain了，无法保证我们生成器的效果）

这就像一个造假币的人和一家造验钞机的厂家，造假币的人造出假币给验钞厂的人，如果失败了他就知道该怎么改进，验钞机也在不断进步，直到最后如果验钞机不能判断那个人造的假币，那么就成功了。

Min Max Game

$$\underset{G}{min}\:\underset{D}{max}\:V(D,G) = \mathbb{E}_{x\sim p_{data}(x)}[log\:D(x)] + \mathbb{E}_{z\sim p_z(z)}[1-log\:D(G(z))]$$

详细的证明写得很清楚这里就不再赘述了。

Algorithm

对于每个iteration：
    对于每k个step：
        从先验噪声p_g(z)中采样m个样本{z1,z2,...,zm}
        从我们的数据分布p_data(z)中取{x1,x2,...,xm}
        更新判别器Discriminator
    从p_g(z)中再次采样m个样本{z1,z2,...,zm}
    更新生成器Generator
# 使用momentum做梯度下降

优势和缺陷

优势：

• 生成了更好的样本
• 理论上来说，可以训练任何一种生成器网络
• 无需设计任何种类的因式分解模型，随便拿来一个生成器和鉴别器都可以用
• 无需设计MC反复采样，无需Inference，回避了近似计算棘手的概率难题

• 和VAE相比，它没有变化的下限。如果鉴别器网络能完美适合，那么这个生成器网络会完美的回复训练分布。也就是说各种对抗式生成网络会渐进一致（asymptotically consistent），而VAE有一定的偏置

缺陷：

• 无法收敛non-convergence
• Collapse Problem：因为没有损失函数，我们的训练只能靠肉眼来判断，很难判断是否在取得进展。在发生崩溃问题时，Generator开始退化，生成相同的样本点，而Discriminator也会对相似的样本点指向相似的方向，导致训练无法继续
• 无需预先建模，模型过于自由不可空。图片变大，维度变多就开始不可控了。所以才会让Discriminator生成k次，Generator才生成1次