Convolutional Network
目的:专门用来处理具有网格结构的数据,如时序数据和图像数据
做法:对于某一时刻或某一位置的值,乘以一个加权函数,得到一个平滑的估计函数。
举例来说,比如我们通过激光传感器可以知道任意时刻一架飞船的位置,其输出为x(t),但是这个值存在噪声干扰。那么为了找到这个飞船位置,我们可以根据其之前的位移做出推测。
其中x(a)就是飞船在a时刻的位移,w(t-a)就是根据a时刻与现在时刻t的久远程度加上的权重。直观上来说,就是a秒钟前在1秒内位移的距离会比a+1秒钟前在1秒内的位移影响更大。
拓展出来,x就是我们的输入,而w就是核函数。
又因为在计算机世界中,数据都是离散discrete的,将积分转化为求和:
那么从一维推广到二维,核K就是w的二维扩展,I就是x的二维输入,而(m,n)就是a的二维扩展,(i,j)就是t的扩展:
又因为其可交换Commutative:
直观的理解就是,I(i-m,j-n)代表了图像上的某一个像素,K(m,n)代表了对应应该乘以的权重。其可交换性就是对K进行了180度的翻转(flip)
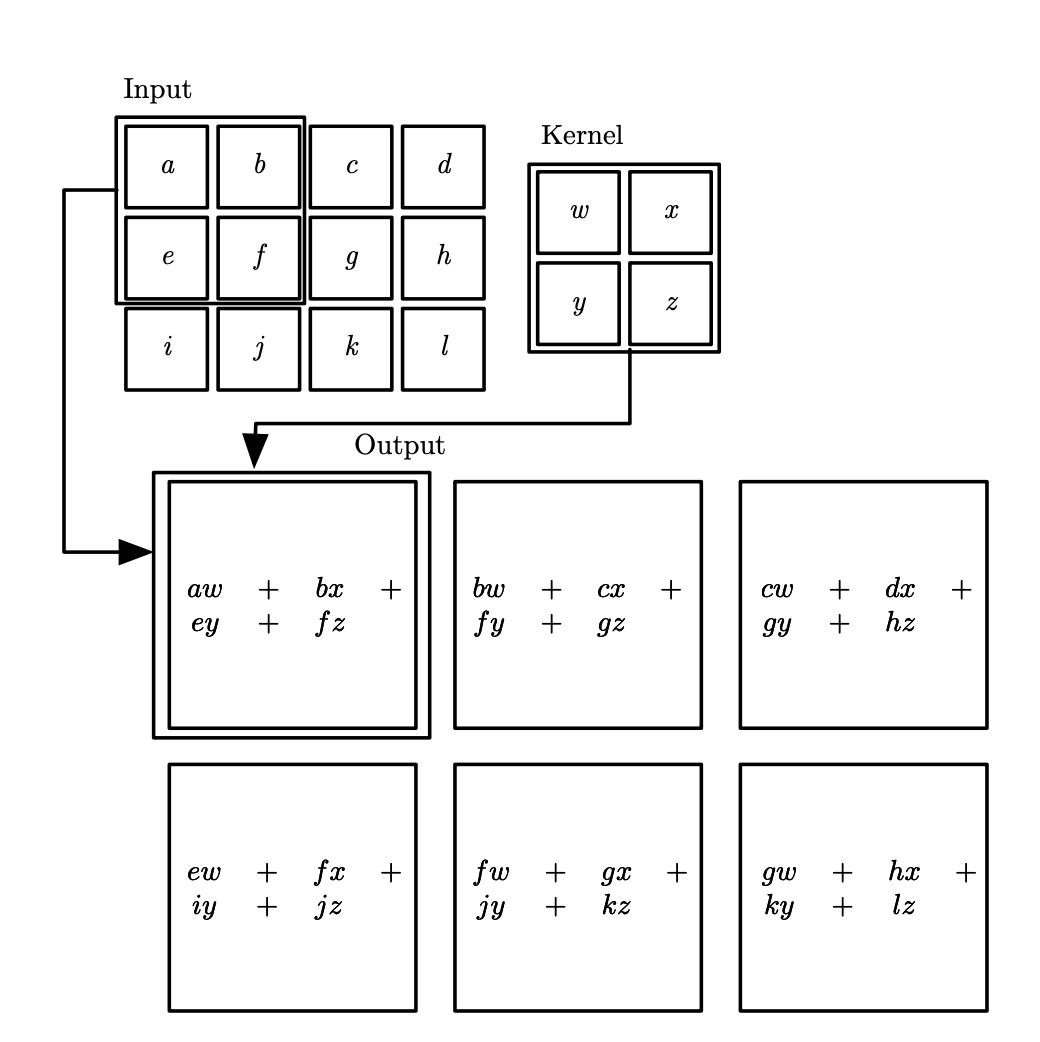
下图为手算例子,摘取自什么!卷积要旋转180度?!
一般用互相关函数(cross-correlation)替代,和卷积运算几乎一样但是并没有对核进行翻转:
卷积定理
在傅立叶变换中,翻转的顺序对卷积结果并不影响,我们因此可以通过交换律从第一个式子得到第二个式子。
又因为卷积具有平移性,我们可以从第二个交换率后的式子得到cross-correlation的式子
- [ 推理于此 ]
动机
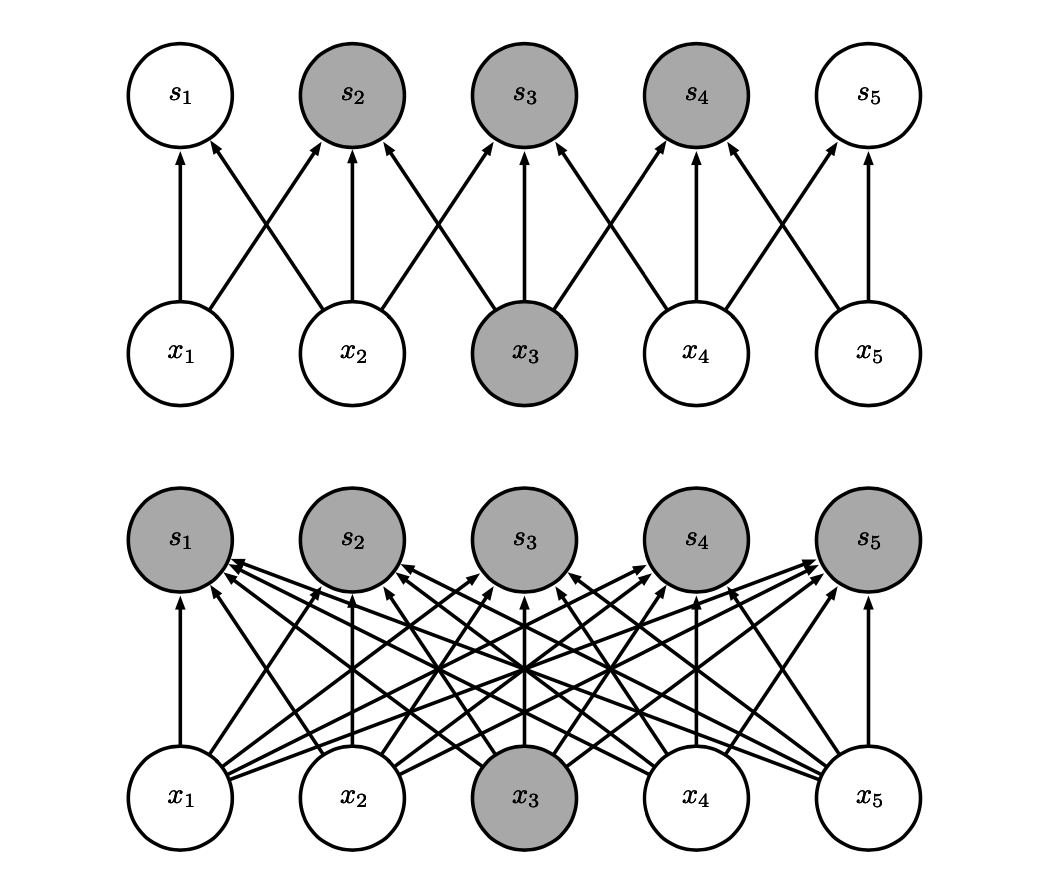
稀疏交互Sparse Interaction
在FNN中输出和输入或者输入和隐藏层之间都是全连接的,这使得每个单独的参数都描述了每一对输入单元和输出单元的交互。
而在CNN中因为Kernel远小于Input的大小,所以只连接自己覆盖的范围。也就具有了sparse的特征。
好处:
- 可以通过少量的核来检测小的但具有意义的特征,比如图像边缘等
- 存储和统计效率提升,比如在fc层中,输入m,输出n的话,需要计算$O(m\times n)$,而如果限制连接数为k则为$O(k \times n)$
参数共享Parameter Sharing
即指公用相同的参数,保证了我们只需学习一个参数集合,而不是每一个输入的每一个权重都要学习。
好处:
- 虽然运行时间依旧是$O(k \times n)$,但是储存的参数降低到k个。
等变表示Equivariant Representation
即指无论我们怎么平移输入数据,卷积都可以检测到那个特征,只是位置变动了。但是卷积对有些变换不是天然等变的,比如缩放和旋转,所有我们通过数据增强的方式,帮助其学习。
池化Pooling
当输入做出少量平移是,池化可以帮助输入的表示近似不变(invariant) 例如,当判定一张图像中是否包含人脸时,我们并不需要知道眼睛的精确像素位置,我们只需要知道有一只眼睛在脸的左边,有一只在右边就行了。
一般运用最大池化(Max Pooling)。其他的池化方法又平均池化(Avg Pooling),$L^2$范数以及基于据中心像素距离的加权平均函数。
不管是什么池化,包括Full Connected是shift invariant。
- 左移一两格,对于3x3的Max Pooling来说无伤大雅,最大值还是会在它的区间内。
- Full Connected因为他们和所有input连接,所以都一样
“使用池化可以看作是增加了一个无限强的先验:这一层学得的函数必须具有对少量平移的不变性。当这个假设成立时,池化可以极大地提高网络的统计效率。”
— Deep Learning
步长和补零
步长可能使我们跳过一些特征,但可以减少计算的开销。其本质相当于对对于正常计算出来的结果进行下采样(downsampling),如下图所示。
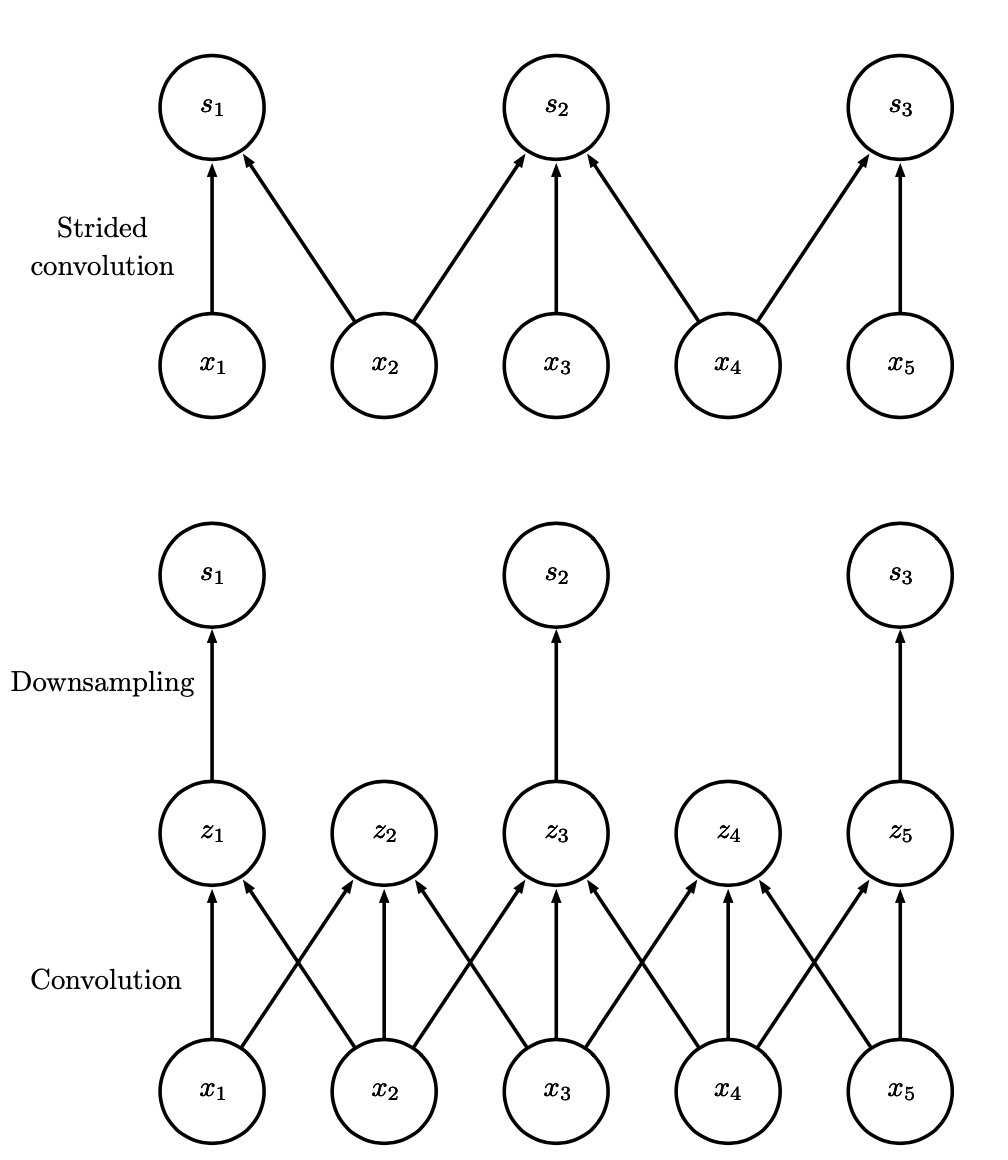
补零就是在左右两边加零,使得可以保留边缘信息。
卷积和池化的上下层关系:
输入大小: $(N, C_{\text{in}}, H, W)$
输出大小: $(N, C_{\text{out}}, H_{\text{out}}, W_{\text{out}})$
高效卷积
对于一个$n \times m \times d$的输入,
普通的做法:用一个$a\times b \times d$的kernel去卷积,则需要
次运算。$O(w^d)$
也可以将其分离(当一个d维的核可以表示成d个向量(每一维一个向量)的外积是,该核被称为可分离的(separable) ),那么可以把原来的核拆成(a,1,d)和(1,b,d)两个向量:
次运算。$O(w\times d)$
一些CNN网络
LeNet-5
最早的CNN网络
AlexNet
- 使用了ReLU
- 使用了数据增强:即随机剪切,旋转,变色等
动量随机梯度下降SGD with momentum:
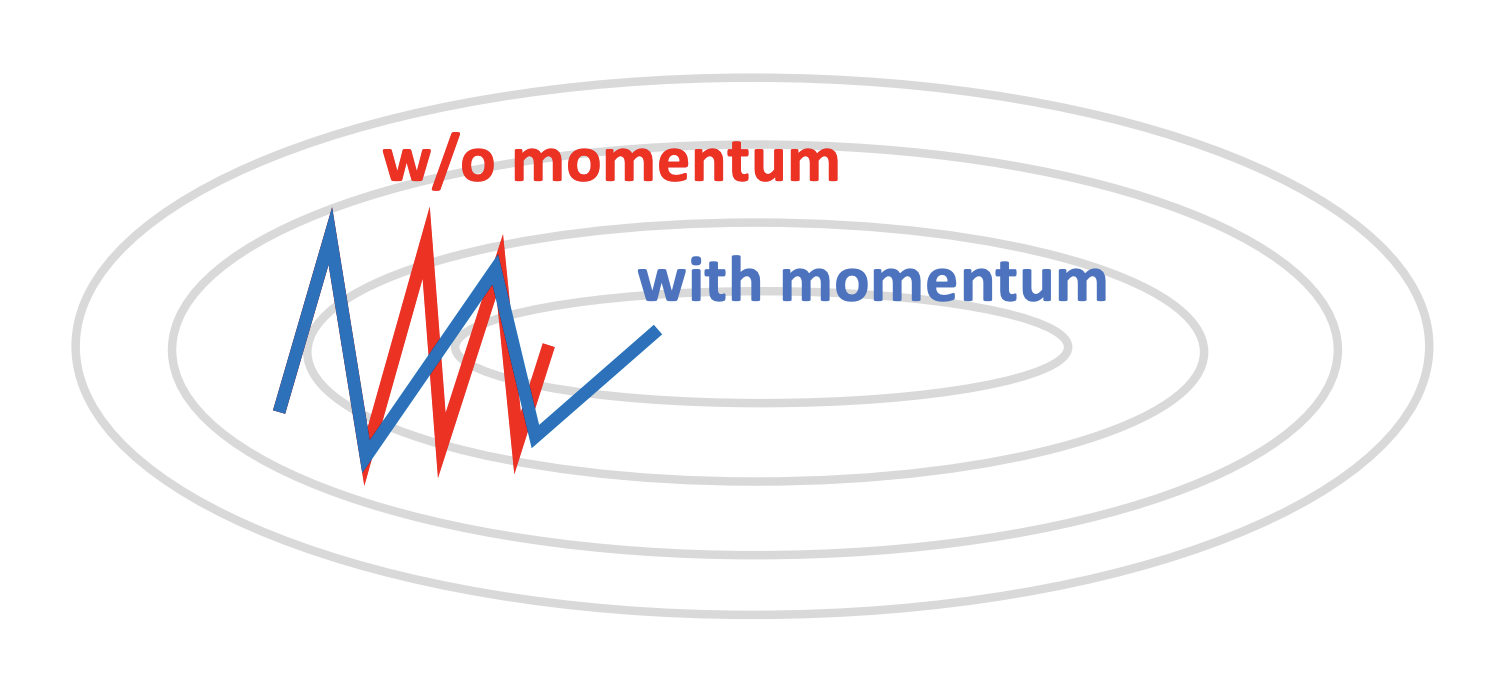
- 没有momentum的话,会导致震荡下降,学习时间很久
我们可以记录上一刻的下降方向和速度即momentum动量,然后乘以k再加上这一刻梯度,那么我们就得到的一个类似等比求和的下降,他会在我们想要的方向上下降的更快
其他梯度下降方法:
- AdaGrad:
设置全局学习率之后,每次通过,全局学习率逐参数的除以历史梯度平方和的平方根,使得每个参数的学习率不同。比如说在,水平方向上梯度越来越大,那随着累加,我们可以渐渐降低learning rate,这样就防止over shoot,增快学习效率。 - RMSProp:
AdaGrad的问题在于learning rate可能提前降低到0。所以对历史梯度乘以k,随着时间的推荐,越早的梯度对现在影响越小,相当于只关注最近一段时间的梯度下降。这样就解决的learning rate提前到零的情况。 - Adam:
同时使用RMSProp和Momentum。Adam 不仅如 RMSProp 算法那样基于一阶矩均值计算适应性参数学习率,它同时还充分利用了梯度的二阶矩均值(即有偏方差uncentered variance)。
- AdaGrad:
- Dropout 是权重衰减weight decay的一种。我们随机忽略一些输入的值(在CNN中一般是在全连接层做这一步),然后计算。
- 直观的理解就是抽学生答问题,没有dropout的话老师会一直抽成绩最好的学生答题。有了dropout我们会随机抽一些一般的同学答题。这样的话全班的水平就有保证了,不会过拟合
- 在机器学习中,为了防止过拟合我们会加入一个惩罚项,一般是所有权重的平方并乘以一个衰减系数
VGG
- 3x3的kernel,因为两个3x3的kernel就可以替代5x5的,这样计算的更快
- 那么既然都用了3x3的kernel,每一层都可以直接复制粘贴就行了
Inception
- Inception Module用极小的核卷积,减少了参数量(30倍小于VGG)
- Factorized Convolution 减少计算
- Batch Normalization:
- Covariate Shift:是指输入数据自带的偏差,导致我们最后学习到的偏差。在机器学习中我们可以normalize,或者白化whiten这些数据
- CNN中,开头输入的数据,结尾我们算得loss,没有batch norm会使得开头输入的变动影响中间所有的权重,使得最后一层一直在变动,学习效率变低。
- 实际不能减少Covariate Shift
- 真正做的是增加噪声,从而达到权重衰减的效果
- $x_i^{‘} = \gamma\frac{x_i-\hat{\mu_i}}{\hat{\sigma_i}} + \beta$ 其中 $\hat{\mu_i}$ 和 $\hat{\sigma_i}$ 是根据minibatch而改变的
- 对minibatch的大小敏感
- 因为都是权重衰减的效果,所以一般不和dropout一起用
ResNet残差网络
我们可以看到现在层数越来越深,ResNet试图回答一个问题,层数越多越好么?答案当然不是,VGG-100的效果和VGG-16的效果差不多,其原因如下图: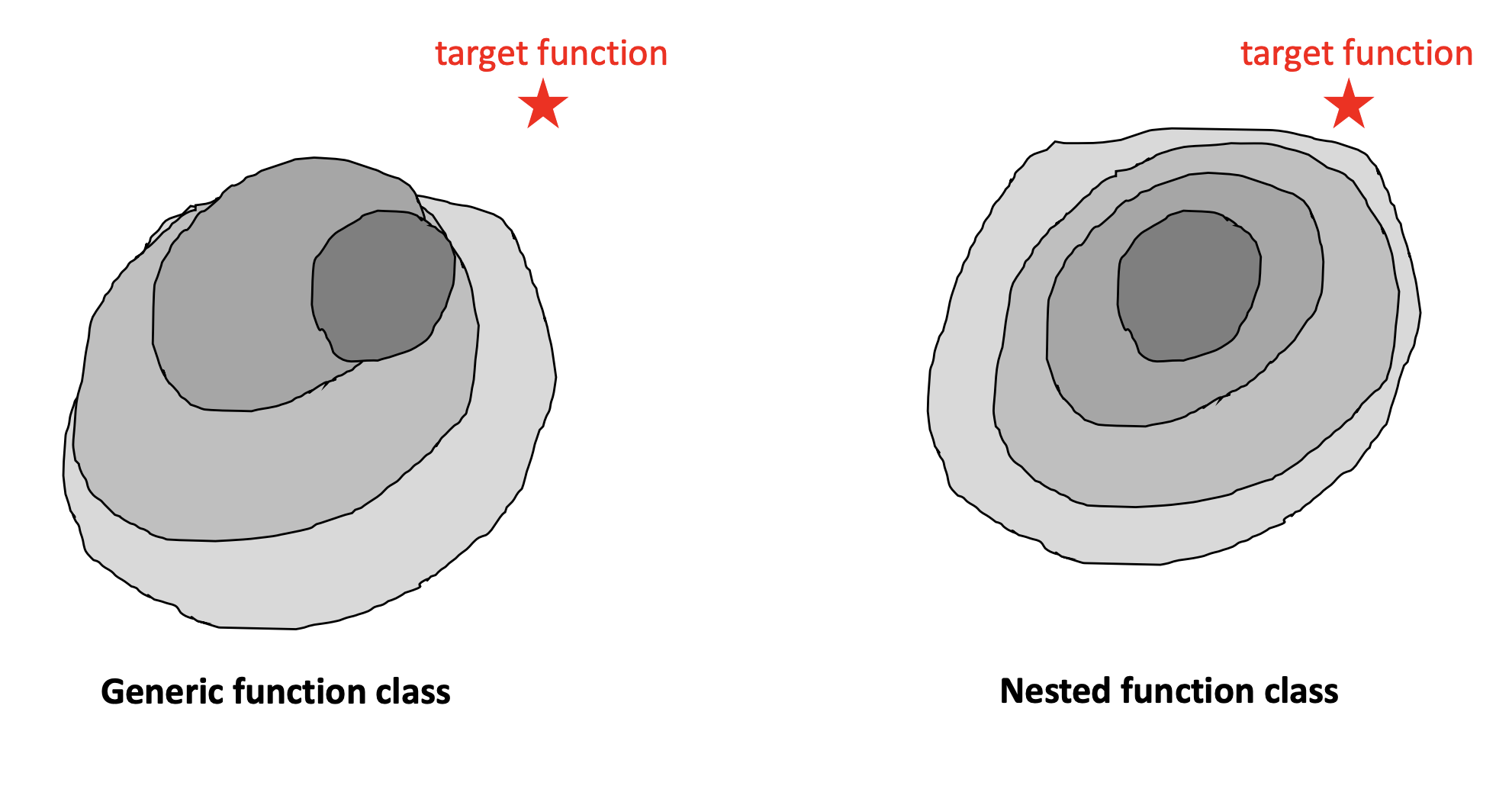
右边是我们希望的效果,也就是从最内层开始,每加一层,可以既包含之前的那一层,又泛化到更多,直到我们包含或接近目标函数。但是实际效果如左图,每加一层并不能全部包含之前的那层,这就使得层数的增加不能保证效果的增加。
而残差网络就是从一层中引出一个输出,直接连到后面的层数上。这样就保证了下一层的效果大于等于这一层。
Neural ODE
- [ 待续 ]