Pyro推断介绍

Posted on

Pyro推断介绍

许多现代的机器学习可以转变为概率推断，继而用像Pyro这样的语言来表达。本章教程的目的，是为一个简单的物理问题创建一个生成模型，使得我们可以用Pyro的推断机制来解决这个问题。不过，我们先来引入本章所需到的模块

1
2
3
4
5
6
7
8
9
import numpy as np
import torch

import pyro
import pyro.infer
import pyro.optim
import pyro.distributions as dist

pyro.set_rng_seed(101)

一个简单的例子

假设我们想要知道某个物体的重量，但是我们手头上的秤并不可靠，每次称重时我们都会得到稍微不同的结果。我们可以通过整合噪音和对这个物体的重量的已知知识（比如它的密度，或者物质构成）来构建这个变量。下面的模型展示了这个过程：

注意，这个模型不仅是我们对于重量的确性程度，也是测量的结果。这个模型对应者下面这个随机函数：

1
2
3
def scale(guess):
    weight = pyro.sample("weight", dist.Normal(guess, 1.0))
    return pyro.sample("measurement", dist.Normal(weight, 0.75))

条件判断Conditioning

概率编程的实际运用在于能够根据观测数据来判断情况从而生成对应模型，并且能够推断出影响生成数据的隐藏因素。在Pyro中，我们通过推断得到一个表达式的估计值，并由此对表达进行区分，这样使得我们可以定下模型，并让它对于不同的观察（observation）进行判断情况。Pyro支持限制模型内部的sample表述等同于一组给定的观察。

再次考虑scale。给定guess = 8.5，假设我们想要从weight的分布中取样，但是现在我们得到的观察结果是measurement == 9.5。那么，我们希望推断下面这个分布：

Pyro提供了函数pyro.condition来让我们限制取样的值。pyro.condition是一个高阶函数，它接受一个模型和一个观察数据的字典（dictionary）的输入，并且返回一个新的模型。该模型拥有相同输入参数和输出签名，但会一直使用观察到的sample得到的值。

1
conditioned_scale = pyro.condition(scale, data={"measurement": 9.5})

因为它表现的就像是普通Python函数，条件判断可以被推迟，或者配合Python的lambda或def被参数化：
1
2
def deferred_conditioned_scale(measurement, guess):
    return pyro.condition(scale, data={"measurement": measurement})(guess)

在某些情况中，将观察（observation）直接传给独立的pyro.sample会比使用pyro.condition更方便。要想如此，可以使用参数obs：

1
2
3
4
def scale_obs(guess):  # equivalent to conditioned_scale above
    weight = pyro.sample("weight", dist.Normal(guess, 1.))
     # here we condition on measurement == 9.5
    return pyro.sample("measurement", dist.Normal(weight, 0.75), obs=9.5)

最后，除了有pyro.condition用来合并观察（observation），Pyro也包括了pyro.do，类似于Pearl的do操作符，独立于pyro.condition之外，用来作因果推断。condition和do可以自由混合或者组合，使得Pyro成为一个建立在模型之上作因果推断的有力工具。

灵活的近似推断和引导函数Guide Function

现在让我们回到conditioned_scale。既然我们有基于观测measurement的条件判断，我们可以用Pyro的近似推断算法来根据guess和measurement == data来估计weight的分布情况。

在Pyro中，推断算法，比如pyro.infer.SVI，让我们能够使用任意的随机函数，我们称之为引导函数（guide functions or guides），作为后验似然分布。引导函数必须满足两个条件才能成为一个模型合格的似然：1. 在模型中所有的没有观察到的（比如，没有被条件判断过的）取样表达式需要出现在引导函数中；2. 引导函数需要和模型有一样的输入签名（比如，接受同样的参数）

引导函数作为可编程的，数据依赖的生成分布/提议分布（proposal distribution）来给重要性采样（importance sampling），拒绝采样（rejection sampling），序列蒙特卡洛（sequential Monte Carlo），马克洛夫链蒙特卡洛（MCMC），和独立的梅特罗波利斯－黑斯廷斯算法（Metropolis–Hastings）用；或者变分分布（variational distributions）或推断网络（inference netowrk）来给随机变分推断（stochastic variational inference）用。目前，重要性采样，MCMC和随机变分推断已经在Pyro中实现了，以后我们也会加入其他的算法。

尽管引导函数的精度的意义对于不同的推断算法而不同，我们应该大致地选择引导函数，这样的话理论上来说，当我们近似模型中未观察到的sample表达式时，就比较灵活了。【？】

在scale这个例子中，结果是，对于给定guess和measurement的weight的真正的后验分布其实是 Normal(9.14， 0.6)。就像建模一样简单，我们可以决定我们感兴趣的后验概率（对于求导，详见(http://www.stat.cmu.edu/~brian/463-663/week09/Chapter%2003.pdf) 3.4章中的例子)

1
2
3
4
def perfect_guide(guess):
    loc =(0.75**2 * guess + 9.5) / (1 + 0.75**2) # 9.14
    scale = np.sqrt(0.75**2/(1 + 0.75**2)) # 0.6
    return pyro.sample("weight", dist.Normal(loc, scale))

参数化的随机函数和变分推断

尽管我们可以写出scale明确的后验分布，但是要明确知道一个引导函数，对于一个任意条件的随机函数的后验分布它是否个好的近似，这也很棘手的。实际上，决定我们定下的真正的后验的随机函数都是特例，而不是规则。比如，在我们的scale中要是使用非线性函数，也会棘手：

1
2
3
def intractable_scale(guess):
    weight = pyro.sample("weight", dist.Normal(guess, 1.0))
    return pyro.sample("measurement", dist.Normal(some_nonlinear_function(weight), 0.75))

我们可以做的，就是使用顶层函数pyro.param来明确一族被命名的参数所索引的引导函数，并搜索这一族中对于一些损失函数最合适的近似。这个来近似后验推断的方法被称之为变分推断。

pyro.param是Pyro key-value参数储存（parameter store）的前端（详见文档）。就像pyro.sample一样，pyro.param被调用时，第一个参数也是其名字。pyro.params第一次被用特定名字调用时，它在参数储存中储存了它的实餐，然后再返回这个值。在那之后，当他在被用该名字调用时，不管其他实餐，他将从参数储存中返回这个值，这和这里的simple_param_store.setdefault类似，但多了一些追踪和管理的功能：

1
2
simple_param_store = {}
a = simple_param_store.setdefault("a", torch.randn(1))

比如，我们可以参数化scale_posterior_guide中的a和b，而不是去手动明确他们：
1
2
3
4
def scale_parametrized_guide(guess):
    a = pyro.param("a", torch.tensor(guess))
    b = pyro.param("b", torch.tensor(1.))
    return pyro.sample("weight", dist.Normal(a, torch.abs(b)))

一方面，注意在scale_posterior_guide中，我们需要对参数b使用torch.abs，因为正态分布的方差必须为正；相似的其他分布也有各自的限制需要被添加。PyTorch的distribution库包括了一个限制模组(constraints module)来强制这些限制，同时把限制加到Pyro的参数中就像传相关的constraint对象给pyro.param一样简单：
1
2
3
4
def scale_parametrized_guide_constrained(guess):
    a = pyro.param("a", torch.tensor(guess))
    b = pyro.param("b", torch.tensor(1.), constraint=constraints.positive)
    return pyro.sample("weight", dist.Normal(a, b))  # no more torch.abs

Pyro就是为了能够使用随机变分推断而建立的。随机变分推断是变分推断中的一个强大的广泛应用的类，它有三个特点：

  1. 参数必须是实数组成的tensor
  2. 我们用模型的执行历史中的samples和引导函数来计算蒙特卡洛估计
  3. 我们用随机梯度下降来寻找最佳参数

通过组合随机梯度下降和PyTorch到的GPU加速的tensor计算以及自动求导功能，我们可以在非常多维的参数空间和大量数据中使用变分推断了。

Pyro的SVI功能会在SVI tutorial中介绍。下面是一个非常简单的例子，运用在scale上：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
guess = 8.5

pyro.clear_param_store()
svi = pyro.infer.SVI(model=conditioned_scale,
                     guide=scale_parametrized_guide,
                     optim=pyro.optim.SGD({"lr": 0.001, "momentum":0.1}),
                     loss=pyro.infer.Trace_ELBO())


losses, a,b  = [], [], []
num_steps = 2500
for t in range(num_steps):
    losses.append(svi.step(guess))
    a.append(pyro.param("a").item())
    b.append(pyro.param("b").item())

plt.plot(losses)
plt.title("ELBO")
plt.xlabel("step")
plt.ylabel("loss");
print('a = ',pyro.param("a").item())
print('b = ', pyro.param("b").item())

输出:

1
2
a =  9.107474327087402
b =  0.6285384893417358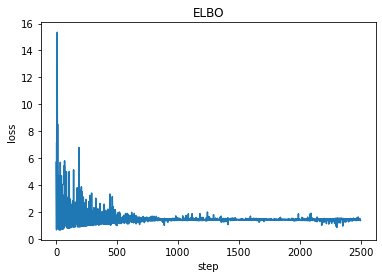

1
2
3
4
5
6
7
8
9
10
plt.subplot(1,2,1)
plt.plot([0,num_steps],[9.14,9.14], 'k:')
plt.plot(a)
plt.ylabel('a')

plt.subplot(1,2,2)
plt.ylabel('b')
plt.plot([0,num_steps],[0.6,0.6], 'k:')
plt.plot(b)
plt.tight_layout()

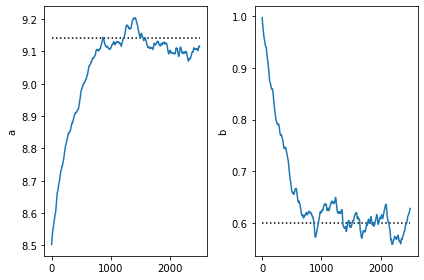
注意，SVI包括参数非常相近到所求条件分布的真实的参数。这是可以预见的，因为我们的引导函数也是从同一个族中出来的。

注意，优化将会更新引导函数参数在参数储存中的值，所以一旦我们找到了好的参数值，我们可以拿从引导函数后验取样重的取样用于后面的任务。

下一步

在变分自动编码器的教程中，我们将见到如何使用深度神经网络来增强类似于scale的模型，如何使用随机变分推断来创建图片的生成模型。